Numpy和数据展示的可视化介绍-萤火

NumPy包是Python生态中用于数据分析、机器学习和科学计算领域的重要工具包。它极大地简化了对向量和矩阵的操作和处理。Python的不少数据处理软件包依赖于NumPy作为其基础架构的核心部分，比如scikit-learn、SciPy、pandas和tensorflow。除了对数值数据进行切片和交叉分析，掌握NumPy也使得开发者在使用各数据处理库调试和处理复杂用例时更具优势。

在本文中，将介绍NumPy的主要用法，以及它如何呈现不同类型的数据（表格，图像，文本等），这些经Numpy处理后的数据将成为机器学习模型的输入。

import numpy as np

Ⅰ. NumPy中的数组操作

1.创建数组

我们可以通过将Python列表传入np.array()来创建一个NumPy数组（也就是强大的ndarray）。在下面的例子里，创建出的数组如右边所示：

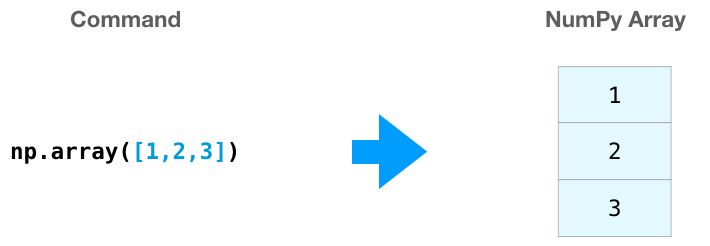
Numpy和数据展示的可视化介绍-萤火

通常情况下，我们希望NumPy为我们初始化数组的值，为此NumPy提供了诸如ones()、zeros()和random.random()之类的方法。我们只需传入元素个数即可：

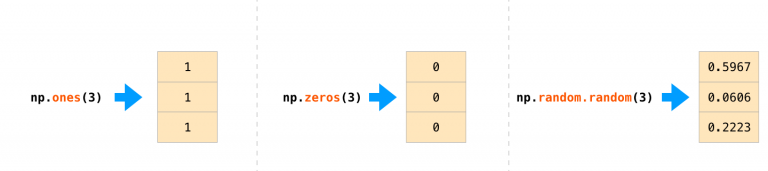
Numpy和数据展示的可视化介绍-萤火

一旦创建好数组后，就可以自由地操纵他们了。

2.数组运算

我们首先创建两个NumPy数组，一个是data数组，另一个是ones数组：

Numpy和数据展示的可视化介绍-萤火

若要计算两个数组的加法，只需简单地敲入data + ones，就可以实现对应位置上的数据相加的操作（即每行数据进行相加），这种操作比循环读取数组的方法代码实现更加简洁。

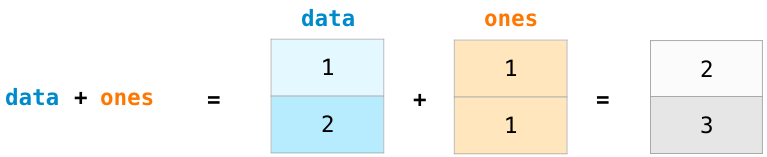
Numpy和数据展示的可视化介绍-萤火

当然，在此基础上举一反三，也可以实现减法、乘法和除法等操作：

Numpy和数据展示的可视化介绍-萤火

许多情况下，我们希望进行数组和单个数值的操作（也称作向量和标量之间的操作）。比如：如果数组表示的是以英里为单位的距离，我们的目标是将其转换为公里数。可以简单的写作data * 1.6：

Numpy和数据展示的可视化介绍-萤火

NumPy通过数组广播（broadcasting）知道这种操作需要和数组的每个元素相乘。

3.数组切片

我们可以像Python列表操作那样对NumPy数组进行索引和切片，如下图所示：

Numpy和数据展示的可视化介绍-萤火

4.聚合函数

NumPy为我们带来的便利还有聚合函数，聚合函数可以将数据进行压缩，统计数组中的一些特征值：

Numpy和数据展示的可视化介绍-萤火

除了min、max和sum函数，还有mean（均值），prod（数据乘法，计算所有元素的乘积），std（标准差），等等。上面的所有例子都在一个维度上处理向量。除此之外，NumPy之美的一个关键之处是它能够将之前所看到的所有函数应用到任意维度上。

Ⅱ. NumPy中的矩阵操作

1.创建矩阵

我们可以通过将二维列表传给Numpy来创建矩阵。

np.array([[1,2],[3,4]])
Numpy和数据展示的可视化介绍-萤火

除此之外，也可以使用上文提到的ones()、zeros()和random.random()来创建矩阵，只需传入一个元组来描述矩阵的维度：

Numpy和数据展示的可视化介绍-萤火

2.矩阵的算术运算

对于大小相同的两个矩阵，我们可以使用算术运算符（+、-、*、/）将其相加或者相乘。NumPy对这类运算采用对应位置（position-wise）操作处理：

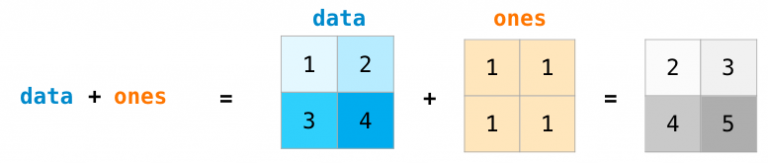
Numpy和数据展示的可视化介绍-萤火

对于不同大小的矩阵，只有其中一个矩阵的维度为1时（例如矩阵只有一列或一行），我们才能进行这些算术运算，在这种情况下，NumPy使用广播（broadcast）进行操作处理：

Numpy和数据展示的可视化介绍-萤火

与算术运算有很大区别是使用点积的矩阵乘法。NumPy提供了dot()方法，可用于矩阵之间进行点积运算：

Numpy和数据展示的可视化介绍-萤火

上图的底部添加了矩阵尺寸，以强调运算的两个矩阵在列和行必须相等。可以将此操作图解为如下所示：

Numpy和数据展示的可视化介绍-萤火

3.矩阵的切片

索引和切片功能在操作矩阵时变得更加有用。可以在不同维度上使用索引操作来对数据进行切片。

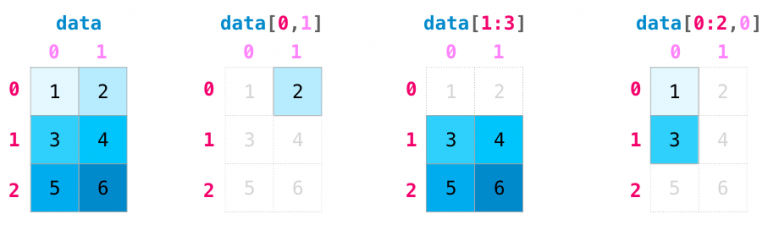
Numpy和数据展示的可视化介绍-萤火

4.矩阵的聚合

我们可以像聚合向量一样聚合矩阵：

Numpy和数据展示的可视化介绍-萤火

不仅可以聚合矩阵中的所有值，还可以使用axis参数指定行和列的聚合：

Numpy和数据展示的可视化介绍-萤火

5.矩阵的转置

处理矩阵时经常需要对矩阵进行转置操作，常见的情况如计算两个矩阵的点积。NumPy数组的属性T可用于获取矩阵的转置。

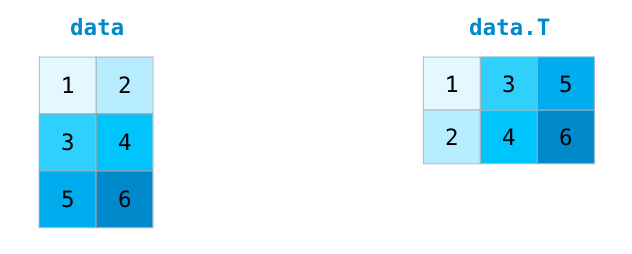
Numpy和数据展示的可视化介绍-萤火

在较为复杂的用例中，你可能会发现自己需要改变某个矩阵的维度。这在机器学习应用中很常见，例如模型的输入矩阵形状与数据集不同，可以使用NumPy的reshape()方法。只需将矩阵所需的新维度传入即可。也可以传入-1，NumPy可以根据你的矩阵推断出正确的维度：

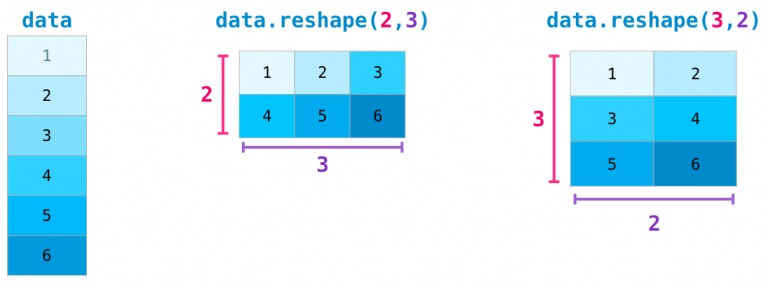
Numpy和数据展示的可视化介绍-萤火

6.高维矩阵

上文中的所有功能都适用于多维数据，其中心数据结构称为ndarray（N维数组）。

Numpy和数据展示的可视化介绍-萤火

很多时候，改变维度只需在NumPy函数的参数中添加一个逗号，如下图所示：

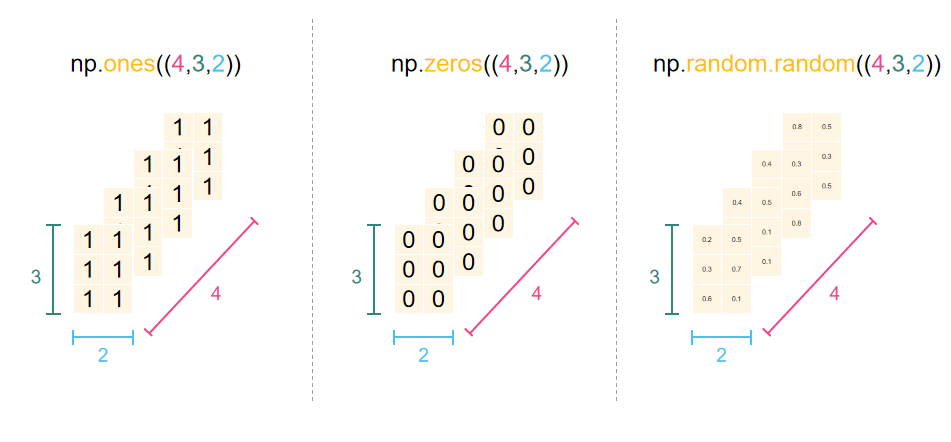
Numpy和数据展示的可视化介绍-萤火

注意：当打印一个3维的NumPy数组时，文本的输出和这里展示的不一样。因为只能在平面上打印出来，NumPy对多维数组的打印顺序是最后一个轴是最快打印的，而第一个是最后打印的。比如，np.ones((4, 3, 2))将会打印如下： 

array([[[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]]])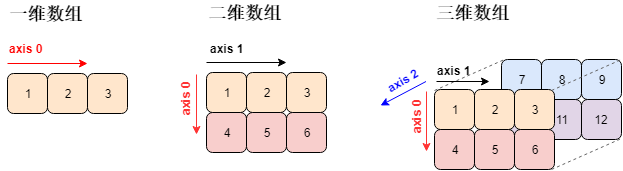
Numpy和数据展示的可视化介绍-萤火
这里三维数组的axis号标错了

注意一个关键字 axis，中文叫「轴」，一个数组是多少维度就有多少轴。由于 Python 计数都是从 0 开始的，那么

  • 第 1 维度 = axis 0
  • 第 2 维度 = axis 1
  • 第 3 维度 = axis 2

但这些数组只可能在平面上打印出来，那么它们 (高于二维的数组) 的表现形式稍微有些不同。

Numpy和数据展示的可视化介绍-萤火

分析上图各个数组的在不同维度上的元素：

  • 一维数组：轴 0 有 3 个元素
  • 二维数组：轴 0 有 2 个元素，轴 1 有 3 个元素
  • 三维数组：轴 0 有 2 个元素 (2 块)，轴 1 有 2 个元素，轴 2 有 3 个元素
  • 四维数组：轴 0 有 2 个元素 (2 块)，轴 1 有 2 个元素 (2 块)，轴 2 有 2 个元素，轴 3 有 3 个元素

Ⅲ. NumPy中的公式应用示例

NumPy的关键用例是实现适用于矩阵和向量的数学公式。这也Python中常用NumPy的原因。例如，均方误差是监督机器学习模型处理回归问题的核心：

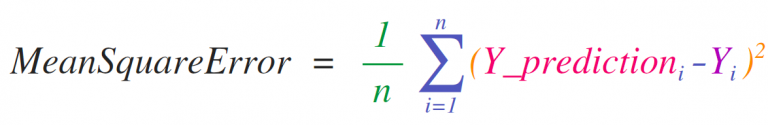
Numpy和数据展示的可视化介绍-萤火

在NumPy中可以很容易地实现均方误差：

Numpy和数据展示的可视化介绍-萤火

这样做的好处是，NumPy无需考虑predictions与labels具体包含的值。我们可以通过如下四个步骤来逐步理解上面的代码：

Numpy和数据展示的可视化介绍-萤火

假设预测（predictions）和标签（labels）向量都包含三个值。这意味着n的值为3。在我们执行减法后，我们最终得到如下值：

Numpy和数据展示的可视化介绍-萤火

然后我们可以计算向量中各值的平方：

Numpy和数据展示的可视化介绍-萤火

现在我们对这些值求和：

Numpy和数据展示的可视化介绍-萤火

最终得到该预测的误差值和模型质量分数。

Ⅳ. 用NumPy表示日常数据

日常接触到的数据类型，如电子表格，图像，音频等等，如何表示呢？NumPy可以解决这个问题。

1.表和电子表格

电子表格或数据表都是二维矩阵。电子表格中的每个工作表都可以是自己的变量。Python中类似的结构是pandas数据帧（dataframe），它实际上使用NumPy来构建的。

Numpy和数据展示的可视化介绍-萤火

2.音频和时间序列

音频文件是一维样本数组。每个样本都是代表一小段音频信号的数字。高质量CD的音频每秒可能有44,100个采样样本，每个样本是一个-65535到65536之间的整数。这意味着如果你有一个10秒的CD质量的WAVE文件，你可以将它加载到长度为10 * 44,100 = 441,000个样本的NumPy数组中。想要提取音频的第一秒？只需将文件加载到我们称之为audio的NumPy数组中，然后截取audio[:44100]。

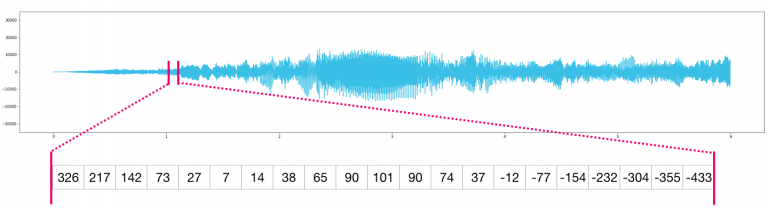
Numpy和数据展示的可视化介绍-萤火

时间序列数据也是如此（例如，股票价格随时间变化的序列）。

3.图像

图像是大小为（高度×宽度）的像素矩阵。如果图像是黑白图像（也称为灰度图像），则每个像素可以由单个数字表示（通常在0（黑色）和255（白色）之间）。如果对图像做处理，裁剪图像的左上角10 x 10大小的一块像素区域，用NumPy中的image[:10,:10]就可以实现。

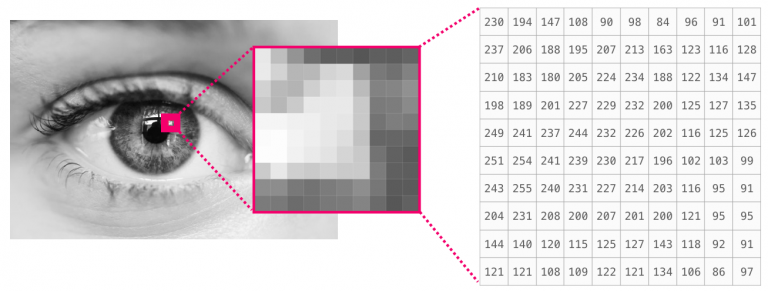
Numpy和数据展示的可视化介绍-萤火

如果图像是彩色的，则每个像素由三个数字表示 ：红色（R），绿色（G）和蓝色（B）。在这种情况下，我们需要第三维（因为每个单元格只能包含一个数字）。因此彩色图像由尺寸为(高 x 宽 x 3）的ndarray表示。

Numpy和数据展示的可视化介绍-萤火

4.语言

如果我们处理文本，情况就会有所不同。用数字表示文本需要两个步骤，构建词汇表（模型知道的所有唯一单词的清单）和嵌入（embedding）。让我们看看用数字表示这个（翻译的）古语引用的步骤：“Have the bards who preceded me left any theme unsung?”

模型需要先训练大量文本才能用数字表示这位战场诗人的诗句。我们可以让模型处理一个小数据集，并使用这个数据集来构建一个词汇表（71,290个单词）：

Numpy和数据展示的可视化介绍-萤火

然后可以将句子划分成一系列“词”token（基于通用规则的单词或单词部分）：

Numpy和数据展示的可视化介绍-萤火

然后我们用词汇表中的id替换每个单词：

Numpy和数据展示的可视化介绍-萤火

这些ID仍然不能为模型提供有价值的信息。因此，在将一系列单词送入模型之前，需要使用嵌入（embedding）来替换token/单词（在本例子中使用50维度的word2vec嵌入)：

Numpy和数据展示的可视化介绍-萤火

你可以看到此NumPy数组的维度为[embedding_dimension x sequence_length]。

在实践中，这些数值不一定是这样的，但我以这种方式呈现它是为了视觉上的一致。出于性能原因，深度学习模型倾向于保留批数据大小的第一维（因为如果并行训练多个示例，则可以更快地训练模型）。很明显，这里非常适合使用reshape()。例如，像BERT这样的模型会期望其输入矩阵的形状为：[batch_size，sequence_length，embedding_size]。

END

参考：
1. A Visual Intro to NumPy and Data Representation
2.这是我见过最好的 NumPy 图解教程！
3.numpy创建三维空数组_Python数据分析基础之NumPy学习 (上)