机器学习入门（4）：归一化

本系列代码托管于：https://github.com/chintsan-code/machine-learning-tutorials

本篇使用的项目为：knnMatch

knn分类器是通过计算特征之间的距离（常用的是欧氏距离，当然也有其他距离的）来实现的，但这样直接计算会带来一个问题：如果一个特征值域范围非常大，那么距离计算就主要取决于这个特征，从而与实际情况相悖（实际结果有可能特征值小的更重要）。因此我们需要做归一化，将所有的数据映射到同一尺度中。

例如在如下的数据集中，前三列代表样本特征，最后一列代表样本标签。可以看出第一列的特征值非常大，明显与后两个不是一个数量级的：

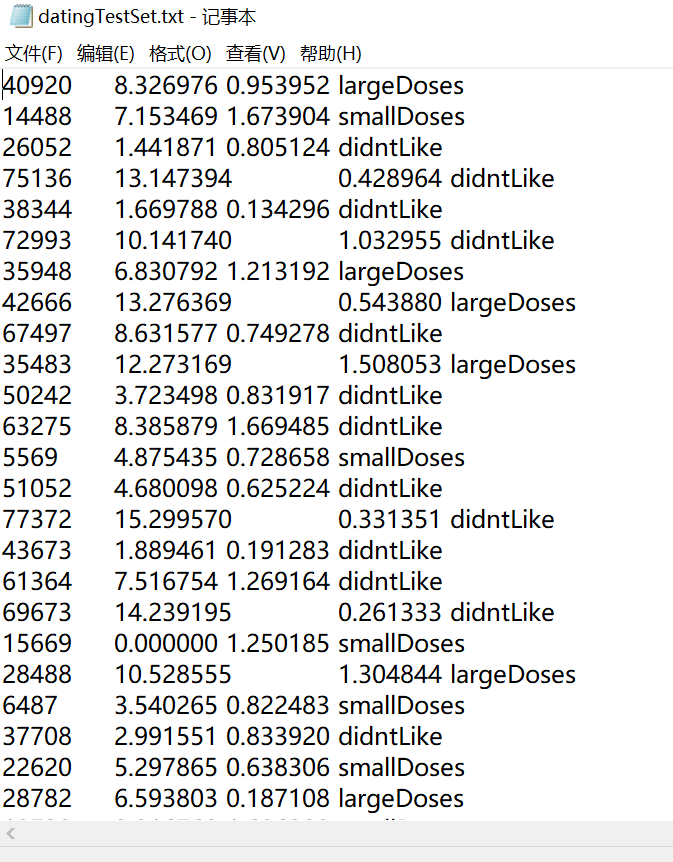
因此我们需要将三个特征值都归一化至[0,1]中。这里我们使用的是最值归一化(MinMaxScaler)

\[x’\ =\ \frac{x\ -\ min\left(x\right)}{max\left(x\right)\ -\ min\left(x\right)}\]

归一化代码：

def autoNorm(dataSet):
    minVals = dataSet.min(0) # 获取dataSet的最小值
    maxVals = dataSet.max(0) # 获取dataSet的最大值
    ranges = maxVals - minVals # max - min，即上面公式的分母
    normDataSet = zeros(shape(dataSet)) 
    m = dataSet.shape[0]
    normDataSet = dataSet - tile(minVals, (m, 1)) # 上面公式的分子
    normDataSet = normDataSet / tile(ranges, (m, 1))  # 归一化后的数据
    return normDataSet, ranges, minVals

这段代码也需要了解numpy的tile函数

再用一个例子结合公式和numpy的tile函数介绍MinMaxScale归一化:

除了最值归一化之外，还有L∞、L1、L2归一化等，在这里不做展开，归一化之后范围是[0, 1]，但并不一定包括0和1，这点要记住，只有最值归一化才一定包含。