一、什么是最小二乘法?
最小二乘法(least squares method),又称最小平方法,是一种数学优化建模方法。它通过最小化误差的平方和寻找数据的最佳函数匹配。 利用最小二乘法可以简便的求得未知的数据,并使得求得的数据与实际数据之间误差的平方和为最小。
“最小二乘法”是对线性方程组,即方程个数比未知数更多的方程组,以回归分析求得近似解的标准方法。在这整个解决方案中,最小二乘法演算为每一方程式的结果中,将残差平方和的总和最小化。
最小平方问题分为两种:线性或普通的最小二乘法,和非线性的最小二乘法,取决于在所有未知数中的残差是否为线性。线性的最小平方问题发生在统计回归分析中;它有一个封闭形式的解决方案。非线性的问题通常经由迭代细致化来解决;在每次迭代中,系统由线性近似,因此在这两种情况下核心演算是相同的 。
本文讨论的是线性最小二乘法。
二、线性最小二乘法的代数求解
先看下面的一个例子:
小明是跑运输的,跑1公里需要6块,跑2公里需要5块(那段时间刚好油价跌了),跑3公里需要7块,跑4公里需要10块,请问跑5公里需要多少块?
已知线性方程组的一般模型为:
$$ \left \{ \begin{array}{c} y_1=wx_1+b \\ y_2=wx_2+b \\ y_3=wx_3+b \\ … \\ y_n=wx_n+b \end{array} \right. $$
毫无疑问,我们最直接想到的就是联立方程组求出w和b,进而得出线性方程
$$y=wx+b$$则问题得解。
那么:
$$ \left \{ \begin{array}{c} 6=w+b \\ 5=2w+b \\ 7=3w+b \\ 10=4w+b \end{array} \right. $$
可以发现,根本解不出w和b!这是为什么呢?原因很简单,我们将数据在图中标出来:
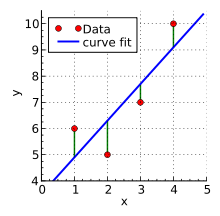
容易看出,找不出一条直线使之完全穿过所有的点。可是现实生活中,我们就希望能找到一条直线,虽然不能满足所有条件,但能近似地表示这个趋势,或者说,能近似地知道5公里的运输成本,这也是有意义的。
最小二乘法也是这样,要尽全力让这条直线最接近这些点,那么问题来了,怎么才叫做最接近呢?直觉告诉我们,这条直线在所有数据点中间穿过,让这些点到这条直线的误差之和越小越好。这里我们用方差来算更客观。也就是说,把每个点到直线的误差平方加起来越小越好:
$$S(w,b)=\sum_{i=1}^{n}{[y_i-(wx_i+b)]^2}$$
在上面的油费问题中,也就是计算当
$$S\left(w,b\right)=[6-(w+b)]^2+[5-(2w+b)]^2+[7-(3w+b)]^2+[10-(4w+b)]^2$$取得最小值时,w和b的值,即为我们想要的 (如果上面的四个方程都能满足,那么S的值显然为0,这是最完美的,但如果做不到完美,我们就让这个S越小越好)
要让S取得最小值(或最大值,但显然这个函数没有最大值:S是开口向上的抛物线),那么S对于w和b分别求偏导结果为0,用一个直观的图来表示:
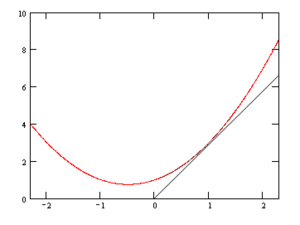
我们看到这条曲线,前半部分是呈下降的趋势,也就是变化率(导数)为负的,后半部分呈上升的趋势,也就是变化率(导数)为正,那么分界点的导数为0,也就是取得最小值的地方。这是一个变量的情况,对于多个变量的情况,要让S取得最小值,那最好是对w和b分别求导(对w求导的时候,把b当常量所以叫求偏导),值为0:
$$ \frac{\partial S}{\partial w}=20b+60w-154=0 $$
$$ \frac{\partial S}{\partial b}=8b+20w-56=0 $$
解上面的方程组:
$$ \left \{ \begin{array}{c} w=1.4 \\ b=3.5 \end{array} \right. $$
也就是$$y=1.4x+3.5$$
这个函数也就是我们要的直线,这条直线虽然不能把那些点串起来,但它能最大程度上接近这些点,将x=5代入,即可求得y=10.5元
三、线性最小二乘法的矩阵求解
还是从上面提到的线性方程组的一般模型开始:
$$ \left \{ \begin{array}{c} y_1=wx_1+b \\ y_2=wx_2+b \\ y_3=wx_3+b \\ … \\ y_n=wx_n+b \end{array} \right. $$
我们也可以使用矩阵来表示:
$$
\begin{bmatrix}
y_1 \\
y_2 \\
y_3 \\
\vdots \\
y_n
\end{bmatrix}
=w
\begin{bmatrix}
x_1 \\
x_2 \\
x_3 \\
\vdots \\
x_n
\end{bmatrix}
+b
\Rightarrow
\begin{bmatrix}
y_1 \\
y_2 \\
y_3 \\
\vdots \\
y_n
\end{bmatrix}
=
\begin{bmatrix}
x_1 & 1 \\
x_2 & 1 \\
x_3 & 1 \\
\vdots \\
x_n & 1
\end{bmatrix}
\begin{bmatrix}
w \\
b
\end{bmatrix}
$$
这里为了方便我们记为
$$XB=Y$$
定义损失函数
$$J(B) = \frac{1}{2}(XB-Y)^T(XB-Y)$$
\( \frac{1}{2} \)在这里主要是为了求导后系数为1,方便计算。根据最小二乘法的原理,我们要对这个损失函数对B向量求导取0。结果如下式:
$$ \frac{\partial J}{\partial B}=X^T(XB-Y)=0$$
对上述求导等式整理后可得:
$$B=(X^TX)^{-1}X^TY$$
其实也可以通过矩阵乘法计算得到:
$$XB=Y \Rightarrow X^TXB=X^TY \Rightarrow B=(X^TX)^{-1}X^TY$$
参考链接:
https://zh.wikipedia.org/wiki/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95
https://www.zhihu.com/question/36324957/answer/255970074
https://zhuanlan.zhihu.com/p/38128785
https://blog.csdn.net/bingfeiqiji/article/details/91443086
https://wenku.baidu.com/view/f7fa307a580216fc700afdb9.html









评论 (0)