使用图解法解下面的线性规划问题 :
$$maxZ=3x_1+5x_2$$
$$ s.t.=\left \{ \begin{array}{c} x_1\le 4 \\ 2x_2\le 12 \\ 3x_1+2x_2\le 18 \\ x_1,x_2\ge 0 \end{array} \right. $$
这个小型问题有两个自变量(\(x_1、x_2\)),仅仅是二维的,因此能够使用图解法来求解。这个过程需要使用 \(x_1\)和\(x_2\) 作为坐标轴构建一个二维图形。第一步通过划定限制条件允许的取值范围的边界线,从而确定限制条件允许的 \((x_1,x_2)\) 的取值。首先,明确非负的限制条件 \(x_1\ge0\)与 \(x_2\ge0\) ,要求 (\(x_1,x_2\))取值位于坐标轴的正面(恰好包括坐标轴在内),即在第一象限。接下来,考虑到限制条件\(x_1\le4\),意味着\(x_1\)的取值不能位于直线\(x_1=4\)的右边(可以使用一个特殊点比如 \( (0,0) \) 帮助判断)。使用同样的方法,在图中画出剩余限制条件的范围。 \((x_1,x_2)\) 的所有允许取值区域被称为可行域(feasible region)
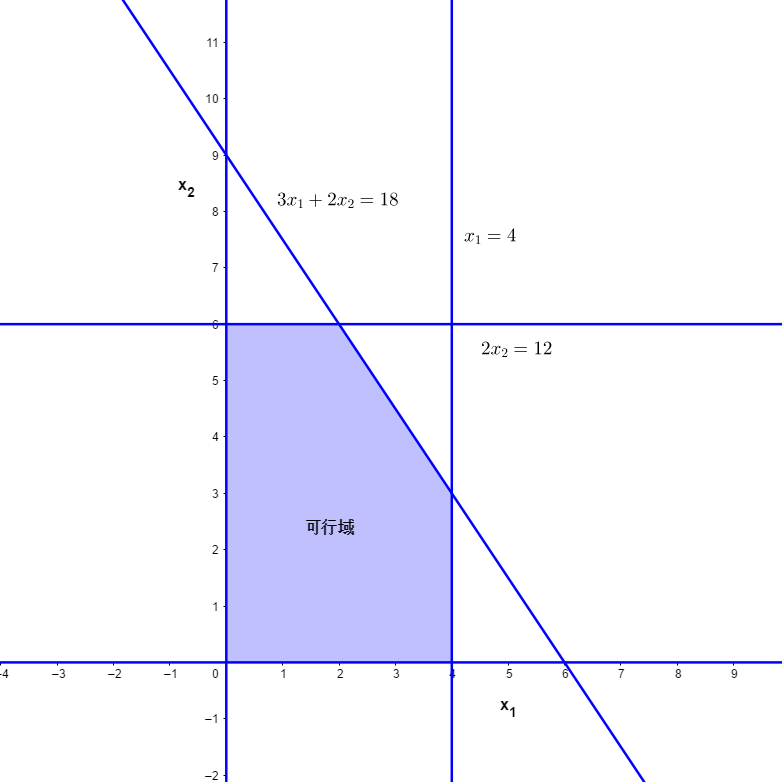
接下来我们要在可行域中选择\((x_1,x_2)\)使目标函数\(Z=3x_1+5x_2\)取得最大值。为了达到这个目的,我们可以将\(Z\)看做一个常数,将目标函数变形为\(x_2\)关于\(x_1\)的截距式(slopc-intercept form)方程:
$$x_2=-\frac{3}{5}x_1+\frac{1}{5}Z$$
它表明直线的斜率是\(-\frac{3}{5}\),同时直线在\(x_2\)轴上的截距式\(\frac{1}{5}Z\),事实上,斜率是固定的\(\frac{3}{5}\)意味着以这种方式绘制的所有直线都是平行的。通过这个截距式方程我们可以得知:截距增加,被选择的\(Z\)也随之增加。这个结果意味着我们可以在下图中反复试验,直到找到一条至少包含可行域中一个点的平行线,这时候取得的\(Z\)就是我们要计算的的目标函数的最大值。
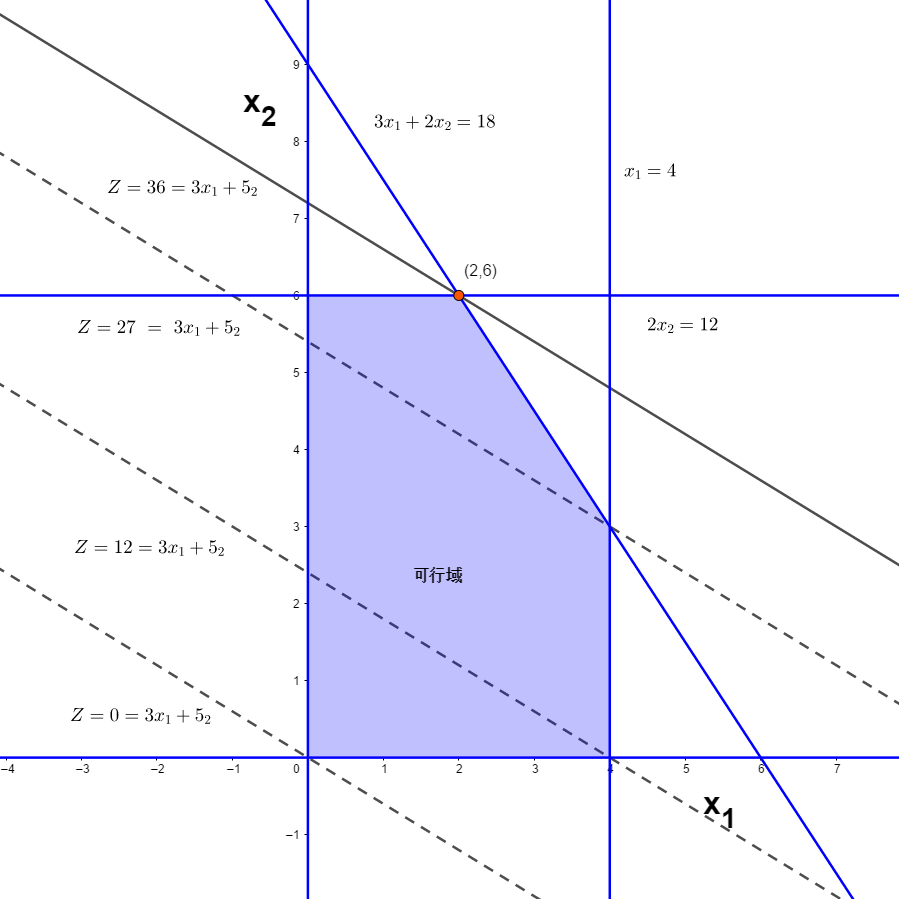
在图中,这样的平行线经过点\((2,6)\),意味着最优解是\(x_1=2,x_2=6\)。将该点带入目标函数中,可以求得
$$Z=3x_1+5x_2=3\times2+5\times6=36$$
以上这个求解的过程就称为图解法。上述问题有唯一最优解。
再看下面这个问题:
$$maxZ=3x_1+4x_2$$
$$ s.t.=\left \{ \begin{array}{c} 2x_1+x_2\le 40 \\ x_1+1.5x_2\le 30 \\ x_1+x_2\ge 50 \\ x_1,x_2\ge 0 \end{array} \right. $$
可以画出可行域:
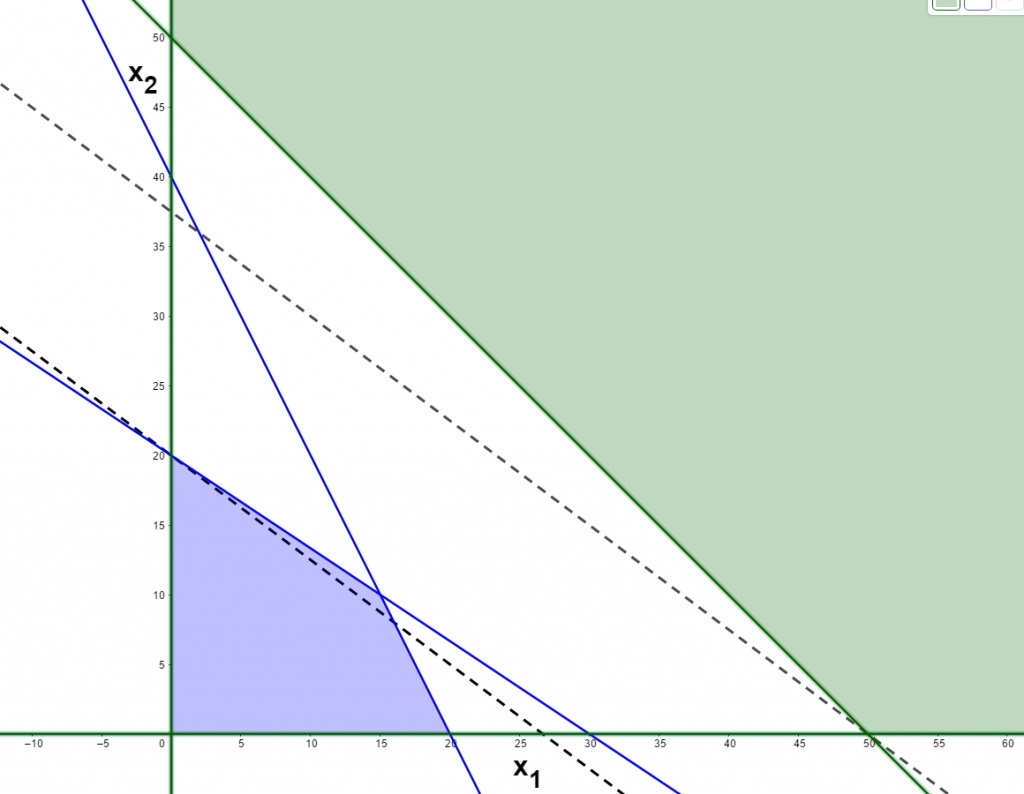
绘制目标函数 , 绘制的图像 , 发现该图像的可行域不存在 , 这种情况属于没有可行解 , 同时也没有最优解。
下面这种情况也属于没有最优解:
$$maxZ=2x_1+x_2$$
$$ s.t.=\left \{ \begin{array}{c} x_1\ge 1 \\ x_1\le 5 \\ x_2\ge 1 \\ x_2\le 5 \\ x_1 \ge 11 \\ x_1 \le 15 \end{array} \right. $$
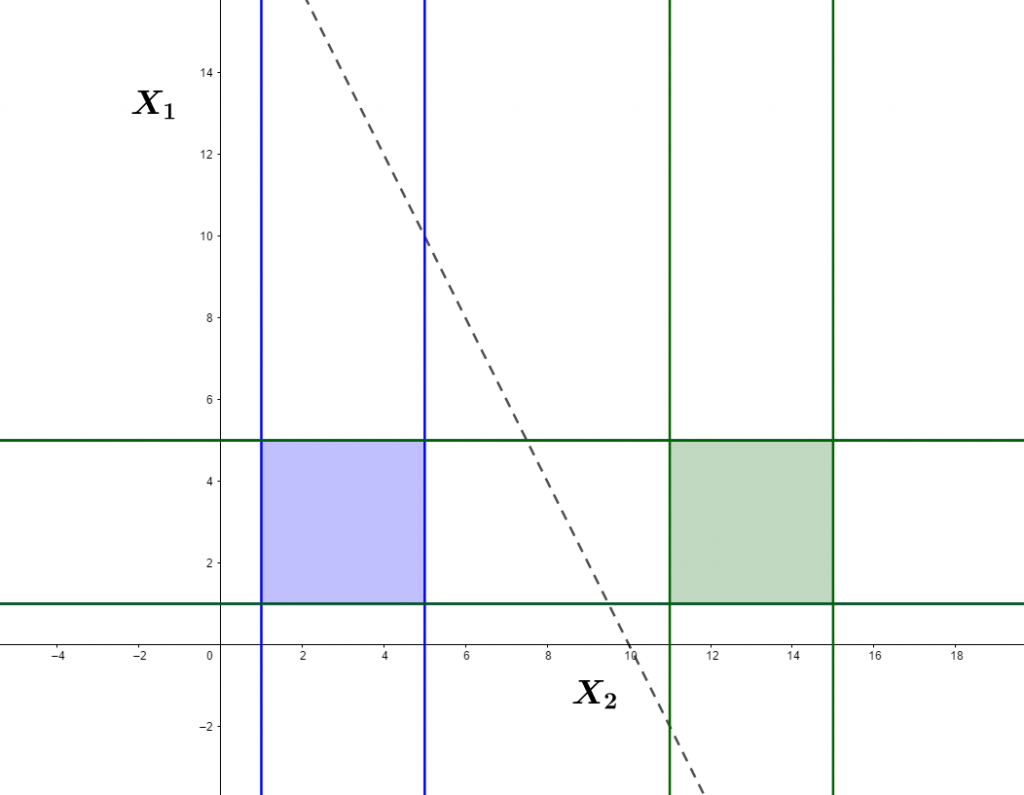
再看下面这个问题:
$$maxZ=x_1+2x_2$$
$$ s.t.=\left \{ \begin{array}{c} x_1+3x_2\ge 6 \\ x_1+x_2\ge 4 \\ 3x_1+x_2\ge 6 \\ x_1,x_2\ge 0 \end{array} \right. $$
可以画出可行域:
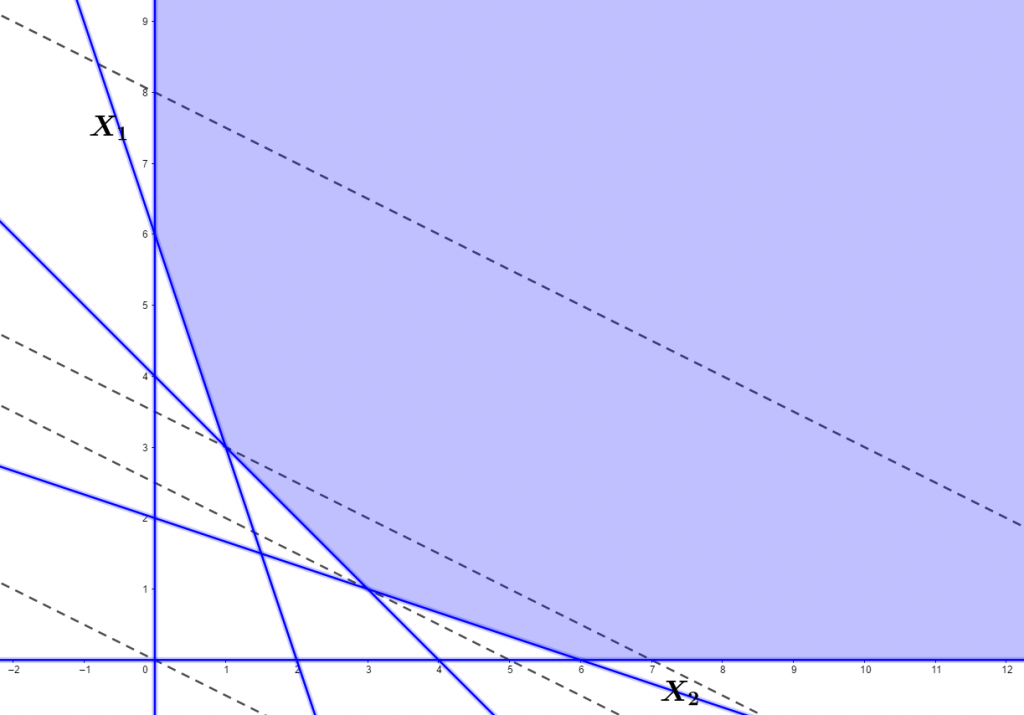
五条直线无法形成一个闭合形区域 , 整体区域是开放的 , 最优解随着\(x_1、x_2\)的增加而增大 , 没有任何限制。(不论 \(x_1、x_2\) 取何值使得 \( Z=z \) , 总存在 \(x’_1、x’_2\) 使得 \( Z=z’ \)且\(z’ \ge z\) )
这种情况下称为线性规划的解是无界解 , 同时也没有最优解 ;
再看下面这个问题:
$$maxZ=3x_1+5.7x_2$$
$$ s.t.=\left \{ \begin{array}{c} x_1+1.9x_2\ge 3.8 \\ x_1-1.9x_2\le 3.8 \\ x_1+1.9x_2\le 11.4 \\ x_1-1.9x_2\ge-3.8 \\ x_1,x_2\ge 0 \end{array} \right. $$
可以画出可行域:
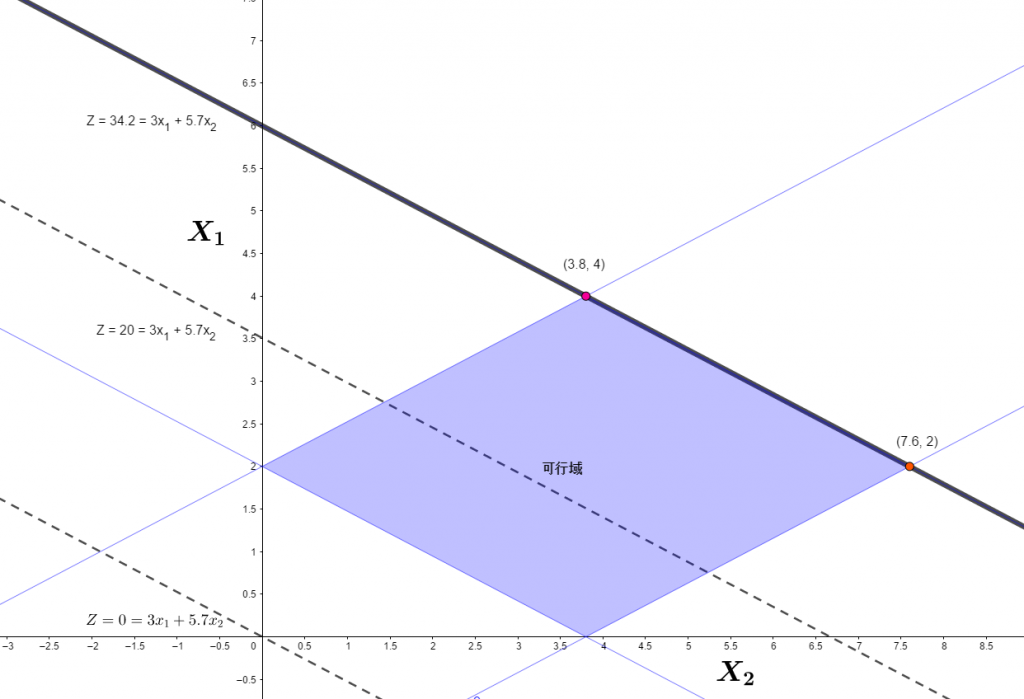
绘制目标函数 , 使其与上述四边形相交 , 取最大值 ,注意该函数图像在坐标系中与可行域边界是平行的 , 即在可行区域内 , 整个线段上所有的点都是最优解 ;
这个最优解的个数是无穷多个 ,相交部分线段上所有点都是最优解。
参考:
1.《运筹学导论》第9版
2.https://blog.csdn.net/shulianghan/article/details/102671536










评论 (0)