本系列代码托管于:https://github.com/chintsan-code/machine-learning-tutorials
本篇使用的项目为:logistic_gradAscent
在之前的篇章,我们讲的knn、决策树、贝叶斯都是通过训练模型(knn不需要训练),输入测试集,得到一个类别,这种叫做分类;回归是也是训练模型,输入测试集,但是得到的是一个数值。所以分类通常用作预测标签,回归通常用作预测数量,但是这也不是绝对的,比如我们也可以用贝叶斯输出一个概率,或者像本篇将要介绍的Logistic回归一样,通常它用来解决二分类问题。
先介绍回归的分类:
回归分为线性回归和非线性回归,线性回归的模型我们很熟悉了,模型是\(y=wx+b\),其中 \(w\) 是权重, \(b\) 是偏置。
线性回归也分为一元线性回归个多元线性回归。一元线性回归的自变量只有一个\(x\)
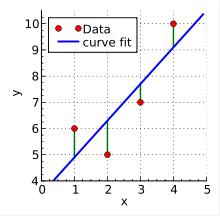
一元线性回归通常用来解决这类问题:通过对输出数据进行拟合,找到一条最优的直线。拟合这条直线通常使用一种非常经典的方法——最小二乘法,更详细的介绍可以看我这篇博文https://blog.linjincan.cn/archives/362
多元线性回归的自变量有多个,其模型为:
$$z=w_1x_1+w_2x_2+…+w_nx_n$$
通过我们将它写成向量的形式:
$$z=
\begin{bmatrix}
w_1 & w_2&…& w_n
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\vdots\\
x_3
\end{bmatrix}
+b
=
\begin{bmatrix}
w_1 & w_2&…& w_n&b
\end{bmatrix}
\begin{bmatrix}
x_1 \\
x_2 \\
\vdots\\
x_n \\
1
\end{bmatrix}
=w^Tx
$$
说完了模型,接下来介绍如何使用Logistic回归解决二分类问题。
二分类,那标签就是{0,1},我们就得想办法,将z映射到{0,1}上,找到一个函数h(x),它的值域是{0,1},z作为输入,也就是h(z(x)),那就搞定了。
我们首先想到的是单位阶跃函数:
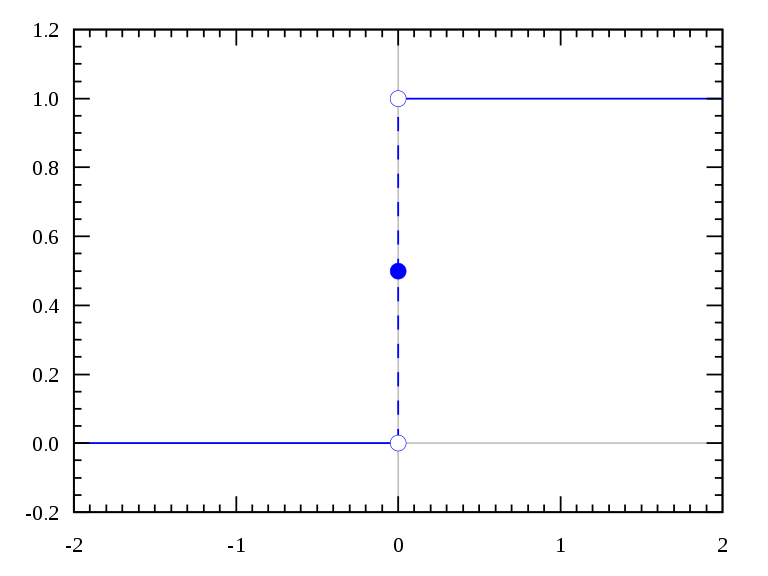
可以看到,不管输入的是什么,都可以输出{0,1}。但是这个函数它不好用,在跳跃点上从0瞬间跳跃到1,也就是这个地方的偏导数不好求,所以我们不用它。这里我们用另一个长得和他挺像的函数:sigmoid
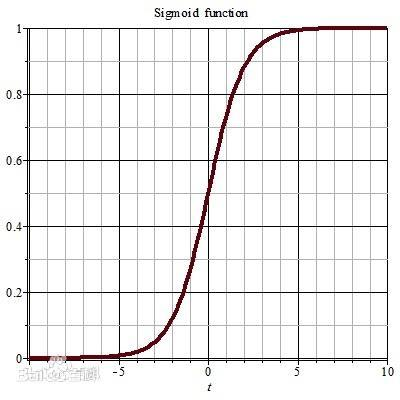
$$h(z)=\frac{1}{1+e^{-z}}$$
sigmoid函数的导数非常有意思,我们可以手动推导一下:
$$h'(z)=\frac{e^{-x}}{(1+e^{-x})^2}=\frac{1}{1+e^{-x}}\times\frac{e^{-x}}{1+e^{-x}}=\frac{1}{1+e^{-x}}\times\frac{1+e^{-x}-1}{1+e^{-x}}\\=\frac{1}{1+e^{-x}}\times(1-\frac{1}{1+e^{-x}})\\=h(x)(1-h(x))$$
前面说到logistic回归主要用来解决二分类问题,也就是样本标签y={0,1},我们假设\(p = P(y=1|x) = h(x)\),那么\(p’=1-p = P(y=0|x)=1-h(x)\),即:
$$
\begin{eqnarray}
P(y|x)=
\begin{cases}
p, &y=1\\
1-p, &y=0
\end{cases}
\end{eqnarray}
\Longrightarrow
P(y|x)=p^y+(1-p)^{1-y}
$$
我们用\(xi、yi\)分别表示某一个样本的输入、输出(标签),即有:
$$ P(y_i|x_i)=p^{y_i}+(1-p)^{1-y_i} $$
假设样本和样本之间是相互独立的,就有:
$$P_总=\prod_{i=1}^{m} P(y_i|x_i)=\prod_{i=1}^{m}(p^{y_i}+(1-p)^{1-y_i})$$
其中,m代表共有m个样本
对等号两边取对数:
$$lnP_总=ln\prod_{i=1}^{m}(p^{y_i}+(1-p)^{1-y_i})=\sum_{i=1}^{m}(y_i lnp+(1-y_i)ln(1-p))$$
我们记L为损失函数:
$$L(w)=lnP_总=\sum_{i=1}^{m}(y_i lnp+(1-y_i)ln(1-p))$$
这里的损失函数的值等于事件发生的总概率,我们希望它越大越好。但是跟损失的含义有点儿违背,所以有人会在前面加一个负号,但是我们这里介绍的是梯度上升法,所以我们不加,如果用梯度下降就加,道理是一样的。
我们的目的就是求\(w\),使得 \( L(w) \) 取得最大值,方法就是让 \( L(w) \) 对 \( w \) 取偏导:
$$\nabla L(w)=\frac{\partial}{\partial w}L(w)= \sum_{i=1}^{m}(y_i\frac{1}{p}p’+(1-y_i)\frac{1}{1-p}(1-p’))\\=\sum_{i=1}^{m}(y_i\frac{1}{p}p(1-p)x_i-(1-y_i)\frac{1}{1-p}p(1-p)x_i)\\=\sum_{i=1}^{m}(y_i(1-p)x_i-(1-y_i)px_i)\\=\sum_{i-1}^{m}((y_i-p)x_i)$$
\( \frac{\partial}{\partial w}L(w) \) 意味着要沿\(w\) 方向移动 。
公式推导完了,我们看代码
# 梯度上升算法
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) # convert to NumPy matrix
labelMat = mat(classLabels).transpose() # convert to NumPy matrix
m, n = shape(dataMatrix)
alpha = 0.001 # 向目标移动的步长
maxCycles = 500 # 迭代次数
weights = ones((n, 1))
for k in range(maxCycles): # heavy on matrix operations
h = sigmoid(dataMatrix * weights) # matrix multi
error = (labelMat - h) # vector subtraction
weights = weights + alpha * dataMatrix.transpose() * error # matrix multi
return weights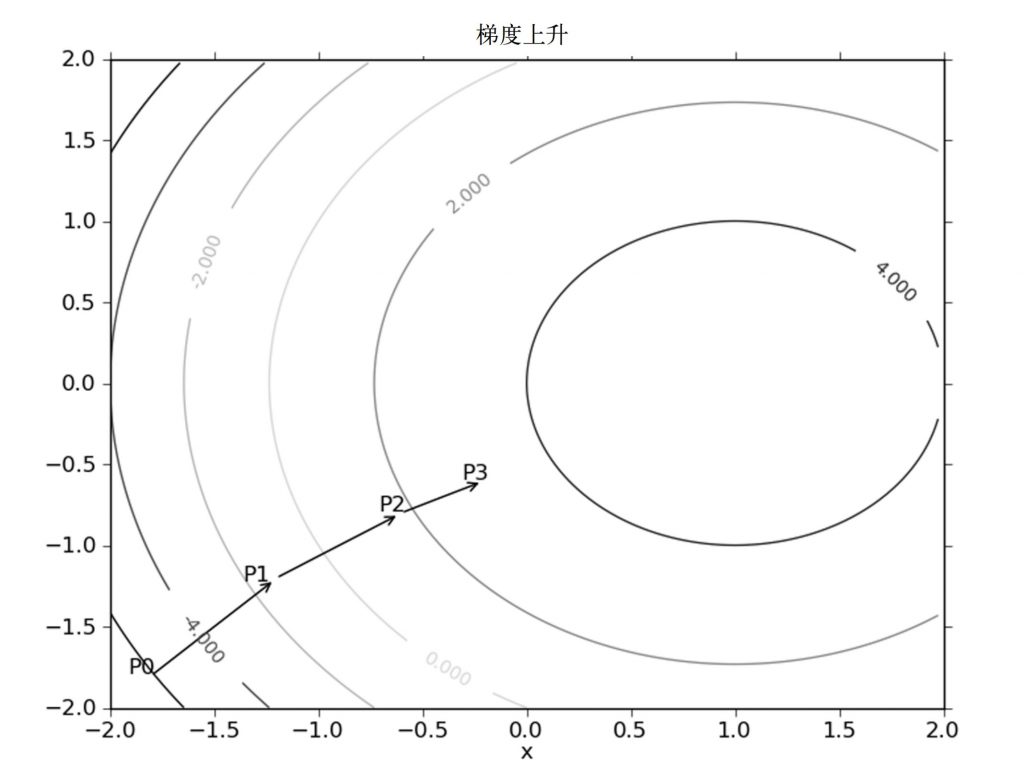
梯度上升算法到达每个点后都会重新估计移动的方向。从P0开始,计算完该点 的梯度,函数就根据梯度移动到下一点P1。在P1点,梯度再次被重新计算 ,并沿新的梯度方向移动到P2。如此循环迭代,直到满足停止条件。迭代的过程中, 梯度算子总是保证我们能选取到最佳的移动方向。
图中的梯度上升算法沿梯度方向移动了一步。可以看到,梯度算子总是指向函数值增长最快的方向。这里所说的是移动方向,而未提到移动量的大小。该量值称为步长,记做\(\alpha\)。 用向量来表示的话,梯度上升算法的迭代公式如下:
$$w=w+\alpha\nabla_w L(w)$$
该公式将一直被迭代执行,直至达到某个停止条件为止,比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围。
代码中的这里alpha对应公式里的 \(\alpha\)
dataMatrix.transpose() * error对应\(\nabla_w L(w) \),也就是\((yi-p)xi\)
labelMat就是 \( yi \) , \( h \) 就是\(p\)
dataMatrix * weights就是 \( z=w^Tx \)
\( h=h(z) \)
运行的结果如下:
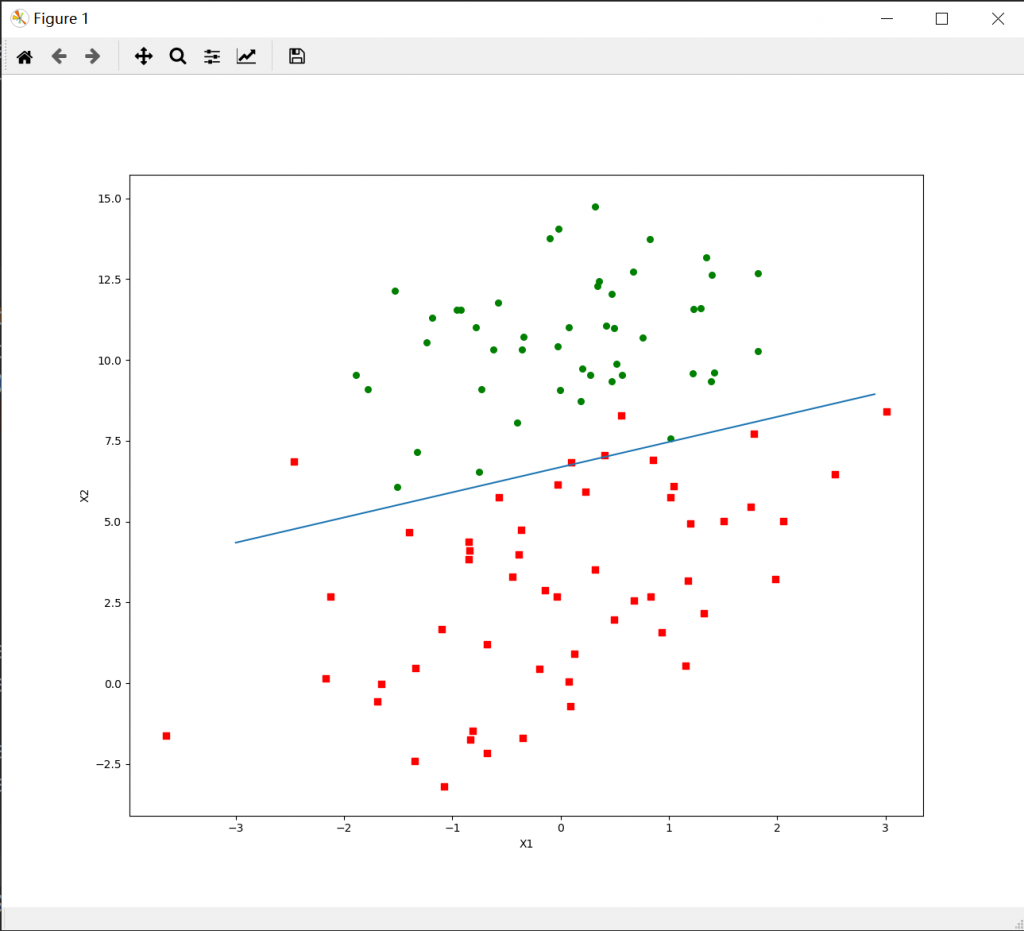
注意其实这里有3个维度,横轴代表 \( x1\),训练集的第一个特征,纵轴代表 \( x2 \) ,训练集的第二个特征,颜色代表 \( z \) ,也就是标签。










评论 (0)