本系列代码托管于:https://github.com/chintsan-code/machine-learning-tutorials
本篇使用的项目为:logistic_stochGradAscentImprove
在上一篇中,我们介绍了Logistics回归和梯度上升算法,再来回顾一下代码:
# 梯度上升算法
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) # convert to NumPy matrix
labelMat = mat(classLabels).transpose() # convert to NumPy matrix
m, n = shape(dataMatrix)
alpha = 0.001 # 向目标移动的步长
maxCycles = 500 # 迭代次数
weights = ones((n, 1))
for k in range(maxCycles): # heavy on matrix operations
h = sigmoid(dataMatrix * weights) # matrix multi
error = (labelMat - h) # vector subtraction
weights = weights + alpha * dataMatrix.transpose() * error # matrix multi
return weights可以看到dataMatrix.transpose()是3*100的向量,error是100*1的向量,所以我们每次迭代都要进行300次乘法。并且,更新回归系数(最优参数)weights时, 都需要遍历整个数据集并对其进行矩阵乘法运算, 这种方法在处理100个左右的数据集时尚可,但如果有数十亿样本和成千上万的特征,那么该方法的计算复杂度就太高了。
一种改进方法是一次仅用一个样本点来更新回归系数,该方法称为随机梯度上升算法。 由于可以在新样本到来时对分类器进行增量式更新,因而随机梯度上升算法是一个在线学习算法。与“在线学习”相对应,一次处理所有数据被称作是“批处理”。 实现的代码如下:
# 随机梯度上升
def stocGradAscent0(dataMatrix, classLabels):
m, n = shape(dataMatrix)
alpha = 0.01
weights = ones(n) # initialize to all ones
for i in range(m):
h = sigmoid(sum(dataMatrix[i] * weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights可以看到,随机梯度上升算法与梯度上升算法在代码上很相似,但也有一些区别:第一,后者的变量h和误差error都是向量(100*1),而前者则全是数值(1*1); 第二,前者没有矩阵的转换过程(convert to NumPy matrix等操作),所有变量的数据类型都是NumPy数组。 运行看下结果如何:
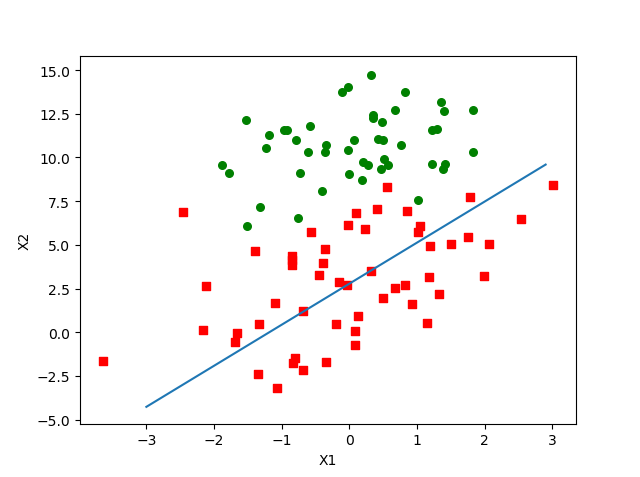
可以看到,拟合出来的直线效果还不错,但效果没有之前批量随机上升算法那么好,大约分错了三分之一的样本,毕竟原先的我们进行了500次迭代,而这里我们只迭代了1次。相同点是两个算法在进行迭代更新回归系数weights时都对数据集中每个样本进行计算。
我们可以继续对该随机梯度上升算法进行改进,加入迭代次数:
# 改进的随机梯度上升
def stocGradAscentInprove(dataMatrix, classLabels, numIter=20):
m, n = shape(dataMatrix)
weights = ones(n) # initialize to all ones
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4 / (1.0 + j + i) + 0.0001 # apha decreases with iteration, does not zero.
randIndex = int(random.uniform(0, len(dataIndex))) # go to 0 because of the constant
h = sigmoid(sum(dataMatrix[randIndex] * weights))
error = classLabels[randIndex] - h
weights = weights + alpha * error * dataMatrix[randIndex]
del (dataIndex[randIndex]) # 删除已迭代元素
return weights与原先的随机上升算法相比,这个程序做了两处改动:
第一,alpha在每次迭代的时候都会调整,会随着迭代次数不断减小,但永远不会减小到0,因为这里还存在一个常数项。必须这样做的原因是为了保证在多次迭代之后新数据仍然具有一定的影响,如果不加常数项,迭代次数/数据集越大,后面的新数据对w调整的就越小(分母越来越大),甚至基本没影响了。(如果要处理的问题是动态变化的,那么可以适当加大上述常数项,来确保新的值获得更大的回归系数)
第二, 更新回归系数(最优参数)时,只使用一个样本点并且选择的样本点是随机的,每次迭代不使用已经用过的样本点。这样的方法,就有效地减少了计算量,并保证了回归效果。
最后让我们看看改进后的算法的运行结果:
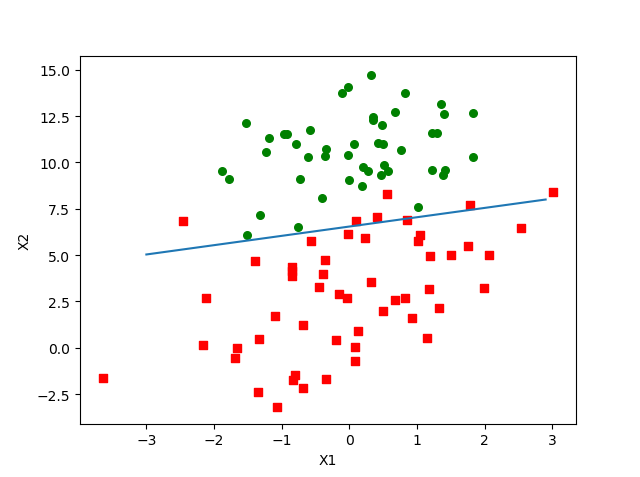
这仅仅是迭代20次的效果,可以看到已经堪比迭代了500次的批量梯度上升算法了,作为对比,我们看下仅迭代20次的批量梯度上升算法的运行结果:











评论 (0)