本系列代码托管于:https://github.com/chintsan-code/machine-learning-tutorials
在介绍SVM这个主题之前,先解释几个概念。 考虑在下图中,能否找到一条直线,将两种数据点分离开来?
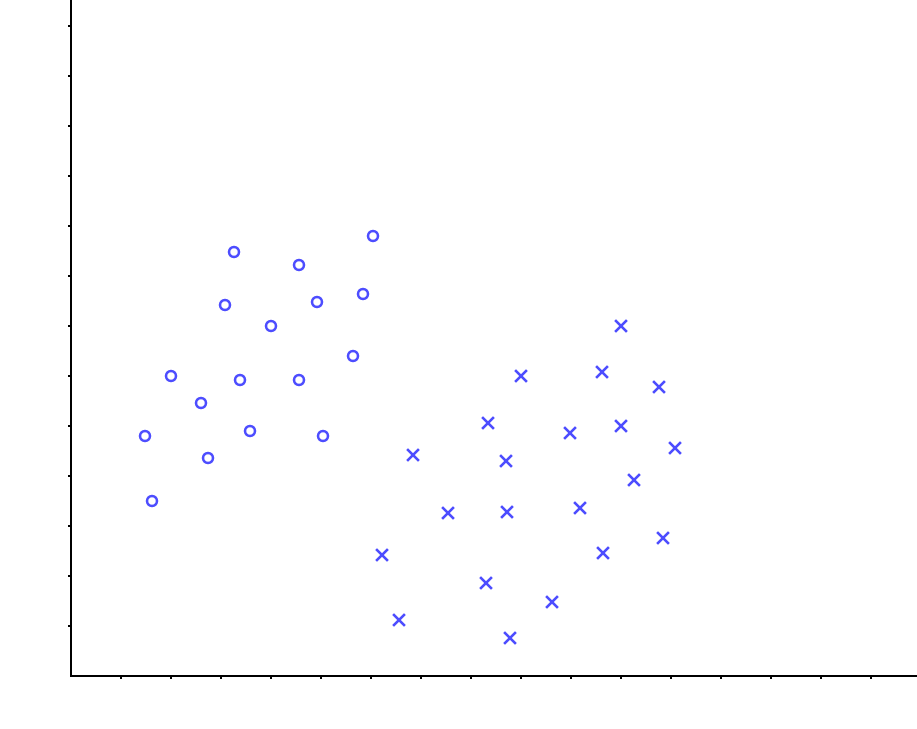
当然可以,且有多种划分方式:
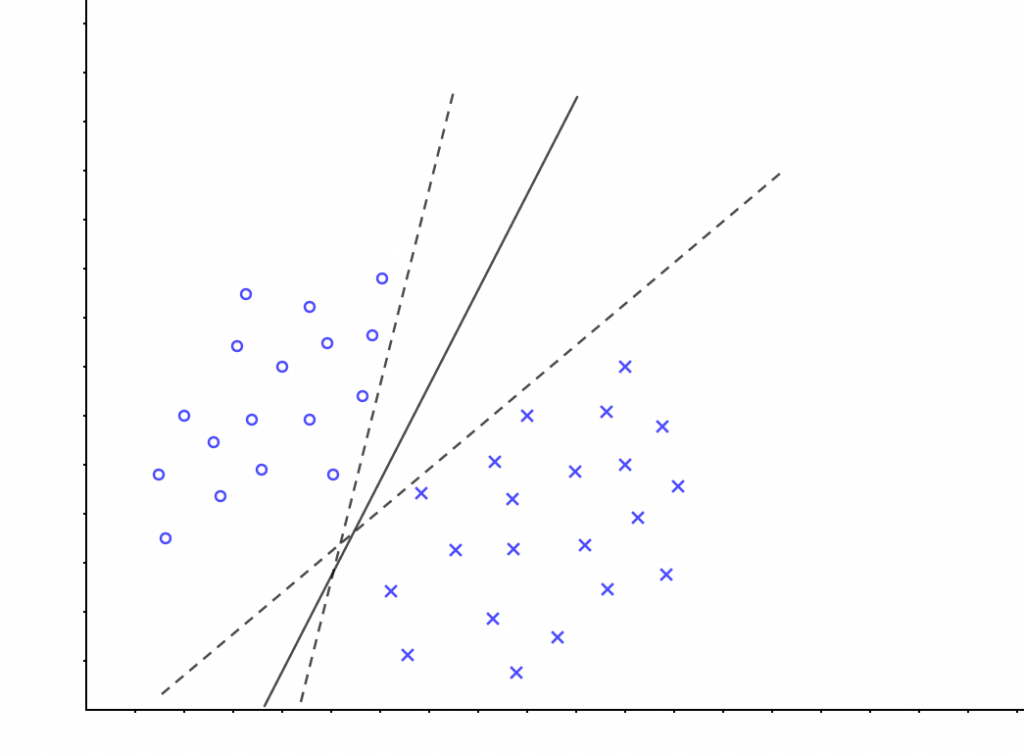
像这样, 将数据集分隔开来的直线称为分隔超平面(separating hyperplane)。 在上面给出的例子中,由于数据点都在二维平面上,所以此时分隔超平面就只是一条直线。但是,如果所给的数据集是三维的,那么此时用来分隔数据的就是一个二维平面。事实上,更高维的情况可以依此类推:如果数据集是N维的,那么就需要一个N-1维的对象来对数据进行分隔。这个N-1维的对象被称为超平面(hyperplane),也就是分类的决策边界。分布在超平面一侧的所有数据都属于某个类别,而分布在另一侧的所有数据则属于另一个类别。(关于超平面可以看另一篇文章:https://blog.linjincan.cn/archives/402)
我们希望能采用这种方式来构建分类器,即如果数据点离决策边界越远,那么其最后的预测结果也就越可信。如在上图中,我们给出了3个超平面用来分隔数据,但其中哪个是最好的呢? 直观上看,应该去找位于两类训练样本“ 正中间 ”的划分超平面, 也就是图中的实线那个。因为该划分超平面对训练样本局部扰动的“容忍”性最好。例如,由于训练集的局限性或噪声的因素,训练集外的样本可能比图中的训练样本更接近两个类的分隔界,这将使许多划分超平面出现错误,而实线的超平面受影响最小。换言之,这个划分超平面所产生的分类结果是最鲁棒的,对未见示例的泛化能力最强。
现在我们的关注点来到了如何找到这条“实线”的问题上来,是不是有点寻找最佳拟合直线的感觉?是的,上述做法确实有点像直线拟合,但这并非最佳方案。我们希望找到离分隔超平面最近的点,确保它们离分隔面的距离尽可能远。这里点到分隔面的距离被称为间隔(margin)。 我们希望间隔尽可能地大,这是因为如果我们犯错或者在有限数据上训练分类器的话,我们希望分类器尽可能健壮。
支持向量(support vector)就是离分隔超平面最近的那些点。接下来要试着最大化支持向量到分隔面的距离,需要找到此问题的优化求解方法。
在\(R^n\)样本空间中,划分超平面可通过如下线性方程来描述:
$$w^Tx+b=0$$
式中\(w=(w_1,w_2,…,w_n)^T\),为法向量,决定了超平面的方向;\(b\)为位移项,决定了超平面与原点之间的距离,显然,划分超平面可被法向量\(w\)和位移\(b\)确定,我们将其记为\((w,b)\),样本空间中任意一点\(x\)到超平面\((w,b)\)的距离可以写为:
$$d=\frac{|w^Tx+b|}{||w||}$$
对于给定的训练样本集\(D=\{(x_1,y_1),(x_2,y_2),…,(x_m,y_m)\},y_i\in\{-1,+1\}\), 假设超平面\((w,b)\)能将训练样本正确分类,即对于\((x_i,y_i)\in D\),若\(y_i=+1\),则有\(w^Tx_i+b>0\);若\(y_i=-1\),则有\(w^Tx_i+b<0\)
这里的类别标签为什么采用-1和+1,而不是0和1呢?这是由于-1和+1仅仅相差一个符号,方便数学上的处理。我们可以通过一个统一公式来表示间隔或者数据点到分隔超平面的距离,同时不必担心数据到底是属于-1还是+1类。
也就是有:
$$y_i=\left \{\begin{array}+1,\hspace{2em}w^Tx_i+b>0\\-1,\hspace{2em}w^Tx_i+b<0\end{array}\right.$$
接下来我们定义在样本空间中的两个点\(x_1、x_2\)(\(x_1、x_2\)为异类支持向量,且分别是各自类别中距离超平面最近的点)到该超平面的距离分别为\(d_1、d_2\),那么有:
$$d_1=\frac{|w^Tx_1+b|}{||w||}$$
$$d_2=\frac{|w^Tx_2+b|}{||w||}$$
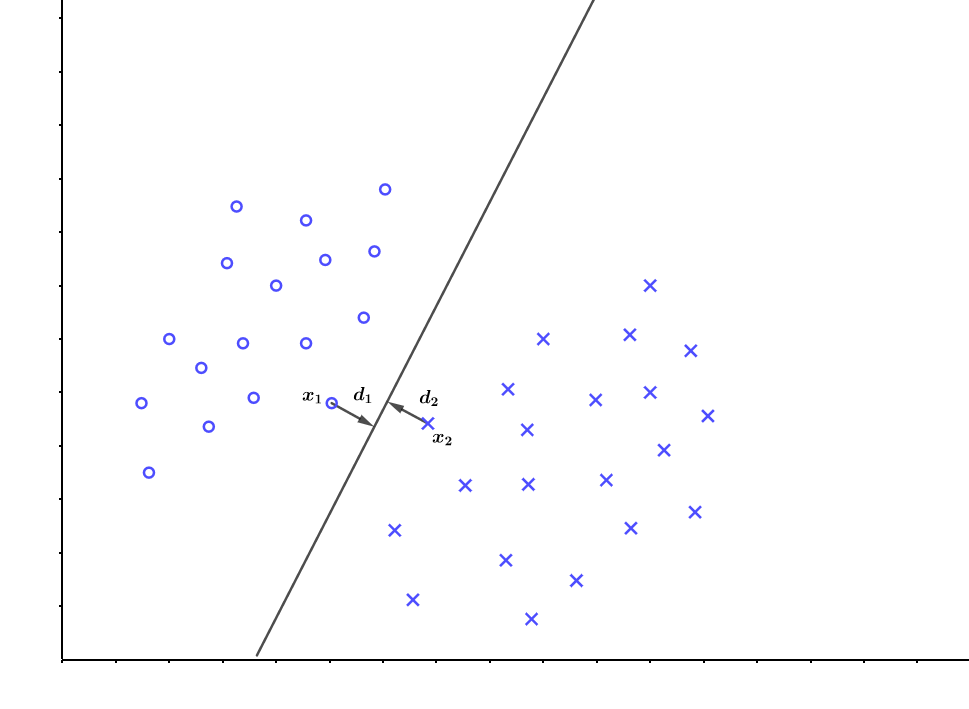
前面说到, 我们希望找到离分隔超平面最近的点,确保它们离分隔面的距离尽可能远,也就是说问题变为求:
$$max D = d_1+d_2= \frac{|w^Tx_1+b|}{||w||} + \frac{|w^Tx_2+b|}{||w||} $$
现在我们已经有了一个超平面\((w,b)\),并且两类中里这个超平面最近的点为\(x_1,x_2\),现在我们继续生成两个平面,它们平行于\((w,b)\)且分别经过\(x_1、x_2\),如下图所示:
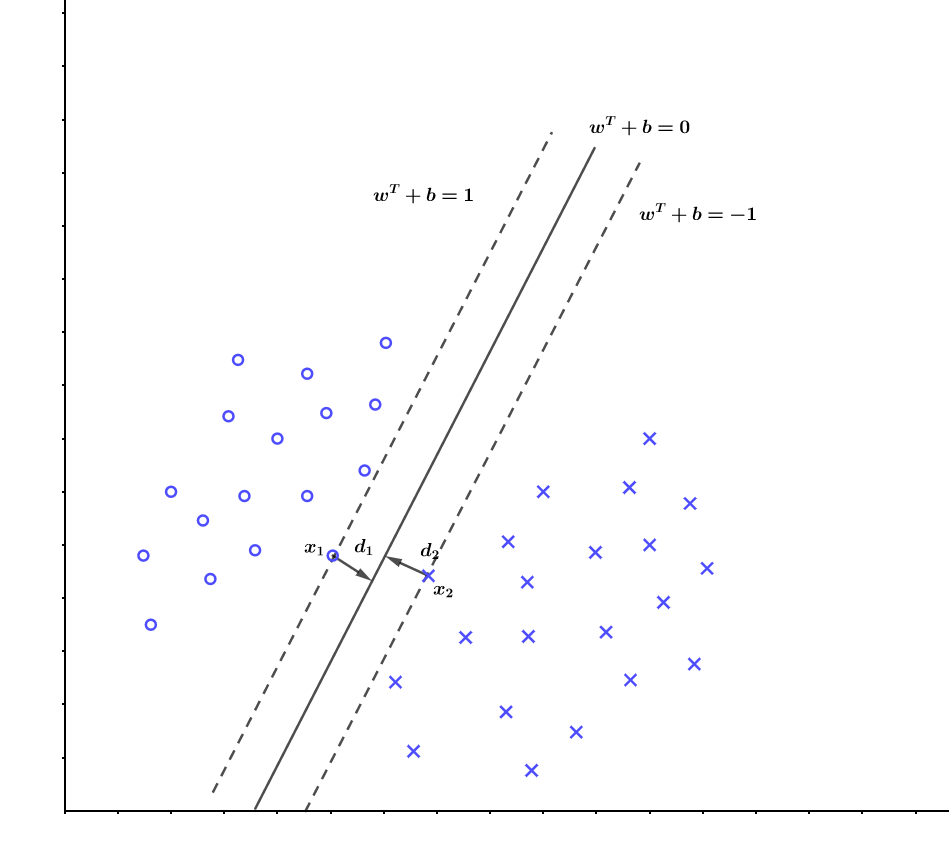
那么真实的分隔超平面我们认为正好就在这两个平面的中间,这样就有\(d_1=d_2\)。因为真实的分隔超平面为\(w^Tx+b=0\),那么我们可以把另外两个平面分别设置为\(w^Tx+b=1\)和\(w^Tx+b=-1\),于是就有:
$$max D= \frac{2}{||w||} $$
为什么我们要设置这两个平面的方程为\(w^Tx+b=1\)和\(w^Tx+b=-1\) 呢?这不就代表了\(d_1=1,d_2=1\)吗?但是我们这时候还不知道\(d_1\)和\(d_2\)到底是多少啊。
确实不知道,那么我们就假设\(d_1=d_2=k,(k>0)\)吧,于是上下两个平面的方程可以写成
$$w^Tx+b=k$$
$$w^Tx+b=-k$$
接着我们对方程两边同时除以k,于是
$$w’^Tx+b’=1$$
$$w’^Tx+b’=-1$$
其中\(w’=\frac{w}{k},b’=\frac{b}{k}\), 可以看到从\(k\)到1,权值无非从\(w\)变化到\(\frac{w}{k}\),\(b\)变到\(\frac{b}{k}\),我们再让\(w=w’,b=b’\),或者说我们去求超平面\(w’^Tx+b’=0\),这不是又回到了起点吗,也就是说,这个中间无非是一个倍数关系。所以我们只需要先确定使得上下等于1的距离,再去找这一组权值,这一组权值会自动变化到一定倍数使得距离为1的。
于是我们求这个超平面\((w,b)\)的问题就转换为:
$$max D= \frac{2}{||w||}$$
$$s.t.\hspace{2em}y_i(w^Tx_i+b)\ge 1,i=1,2,3,…,n$$
其中约束条件就是之前得到的这条式子而来:
$$y_i=\left \{\begin{array}+1,\hspace{2em}w^Tx_i+b>0\\-1,\hspace{2em}w^Tx_i+b<0\end{array}\right.$$
显然,为了最大化间隔,仅需最大化\(\frac{1}{||w||}\)即可,这等价于最小化\(||w||^2\),于是,问题也可以转化为一个含有不等式约束的凸二次规划问题 :
$$min \frac{1}{2}||w||^2$$
$$s.t.\hspace{2em}y_i(w^Tx_i+b)\ge 1,i=1,2,3,…,n$$
这就是支持向量机(Support Vector Machine ,简称 SVM)的基本型。
- 参考:
- 《机器学习实战》 [美]Peter Harrington著,李锐、李鹏、曲亚东、王斌 译
- 《机器学习》 周志华著
- 学习SVM,这篇文章就够了!(附详细代码)










评论 (0)