本系列代码托管于:https://github.com/chintsan-code/machine-learning-tutorials
本篇使用的项目为:standRegrs
在之前的文章中(机器学习入门(12)——Logistic回归(梯度上升算法))我们已经介绍了线性回归,但之前我们是用它来解决分类问题(借助Sigmoid函数),本文将介绍回归的另一种主流用法:预测数值。
首先给出线性回归的基本模型:
$$
y=w^TX(或者写做y=X^Tw)
$$
假定输入数据存放在矩阵\(X\)中,而回归系数存放在向量\(w\)中。那么对于给定的数据\(x_1\),预测的结果将会通过\(y_1=x_1^Tw\)给出。我们的目标就是从现有数据集中的\(X\)及其对应的\(y\),找到回归系数\(w\)。一个常用的方法就是找出使预测\(y\)值和真实\(y\)值误差最小的\(w\),通过我们使用平方误差。(之所以不用简单的累加是因为正负值误差会相互抵消)
平方误差和可以写做:
$$
\sum_{i=1}^{m}{(y_i-x_i^Tw)^2}
$$
用矩阵表示还可以写做\((y-Xw)^T(y-Xw)\),如果对\(w\)求导,得到\(X^T(Y-Xw)\),令其等于零,解出\(w\)如下:
$$
\hat{w}=(X^TX)^{-1}X^Ty
$$
\(\hat{w}\)表示这是当前可以估计出的\(w\)的最优解。从现有数据上估计出的\(w\)可能并不是数据中的真实\(w\)值,所以这里使用了一个\(\hat{}\)符号来表示它仅是\(w\)的一个最佳估计。
值得注意的是,上述公式中包含\((X^TX)^{-1}\),也就是需要对矩阵求逆,因此这个方程只在逆矩阵存在的时候适用。然而,矩阵的逆可能并不存在,因此必须要在代码中对此作出判断。
上述的最佳\(w\)求解是统计学中的常见问题,除了矩阵方法外还有很多其他方法可以解决。通过调用NumPy库里的矩阵方法,我们可以仅使用几行代码就完成所需功能。该方法也称作OLS,意思是“普通最小二乘法”(ordinary least squares)。
def standRegres(xArr, yArr):
xMat = mat(xArr)
yMat = mat(yArr).T
xTx = xMat.T * xMat
if linalg.det(xTx) == 0.0:
print("This matrix is singular, cannot do inverse")
return
ws = xTx.I * (xMat.T * yMat)
return wsstandRegres()函数用来计算最佳拟合直线。该函数首先读入\(X\)和\(y\)并将它们保存到矩阵中;然后计算\(X^TX\),然后判断它的行列式是否为零,如果行列式为零,那么计算逆矩阵的时候将出现错误。NumPy提供一个线性代数的库linalg,其中包含很多有用的函数,可以直接调用linalg.det()来计算行列式。最后,如果行列式非零,计算并返回\(w\)。如果没有检查行列式是否为零就试图计算矩阵的逆,将会出现错误。NumPy的线性代数库还提供一个函数来解未知矩阵,如果使用该函数,那么代码ws = xTx.I * (xMat.T * yMat)应写成ws=linalg.solve(xTx, xMat.T*yMat)
从给定的数据集中我们可以看出,第一个值总为1.0,即\(x_0=1.0\),这是因为我们假定了偏移量是一个常数(即\(ws[0] = b\))。变量\(ws\)存放的就是回归系数。在用内积来预测\(y\)的时候,\(ws\)的第一维将乘以常数\(x_0\)。于是有\(y=ws[0]+ws[1]*x_1\)。这里的\(y\)是预测出来的,为了将它和真实值区分开来,下面我们用\(yHat\)表示它。
运行程序:
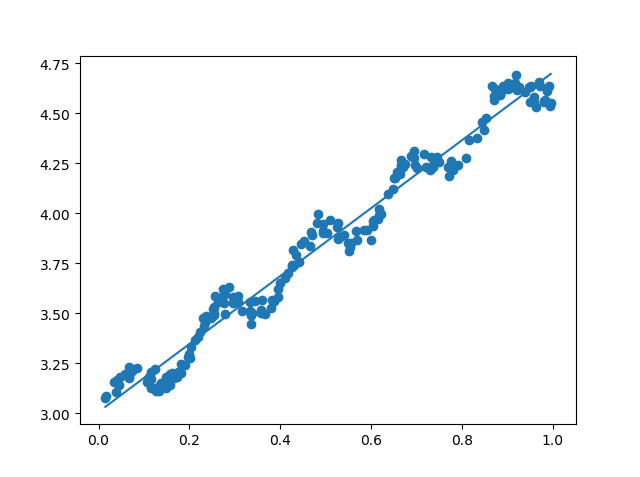
通过计算预测值yHat序列和真实值y序列的相关系数,可以得到他们的匹配程度。
在Python中,NumPy库提供了相关系数的计算方法:可以通过命令corrcoef(yEstimate, yActual)来计算预测值和真实值的相关性。
# 计算相关系数
def calcCorrcoef(xArr, yArr, ws):
xMat = mat(xArr)
yMat = mat(yArr)
yHat = xMat * ws
return corrcoef(yHat.T, yMat)输出结果为[[1. 0.98647356]
[0.98647356 1. ]]
该矩阵包含所有两两组合的相关系数。可以看到,对角线上的数据是1.0,因为yMat和自己的匹配是最完美的,而\(yHat\)和\(yMat\)的相关系数为0.98。
- 参考
- 《机器学习实战》 [美]Peter Harrington著,李锐、李鹏、曲亚东、王斌 译










评论 (0)