本系列代码托管于:https://github.com/chintsan-code/machine-learning-tutorials
本篇使用的项目为:tree_splitDataset
我们经常使用决策树处理分类问题,近来的调查表明决策树也是最经常使用的数据挖掘算法。 它之所以如此流行,一个很重要的原因就是不需要了解机器学习的知识,就能搞明白决策树是如何工作的。
如果你以前没有接触过决策树,完全不用担心,它的概念非常简单。即使不知道它也可以通 过简单的图形了解其工作原理,图3-1所示的流程图就是一个决策树,长方形代表判断模块 (decision block),椭圆形代表终止模块(terminating block),表示已经得出结论,可以终止运行。 从判断模块引出的左右箭头称作分支(branch),它可以到达另一个判断模块或者终止模块 。
首先来看下面一个数据集:
| 不浮出水面是否可以生存 | 是否有脚蹼 | 属于鱼类 | |
| 1 | 是 | 是 | 是 |
| 2 | 是 | 是 | 是 |
| 3 | 是 | 否 | 否 |
| 4 | 否 | 是 | 否 |
| 5 | 否 | 是 | 否 |
(数据集中数字1-5表示样本编号,“ 不浮出水面是否可以生存 ”和“ 是否有脚蹼 ” 表示两个特征,“ 属于鱼类 ”表示标签。)
对于这个数据集,我们有如下两种划分的方法:
1.先按特征“ 不浮出水面是否可以生存 ”划分:
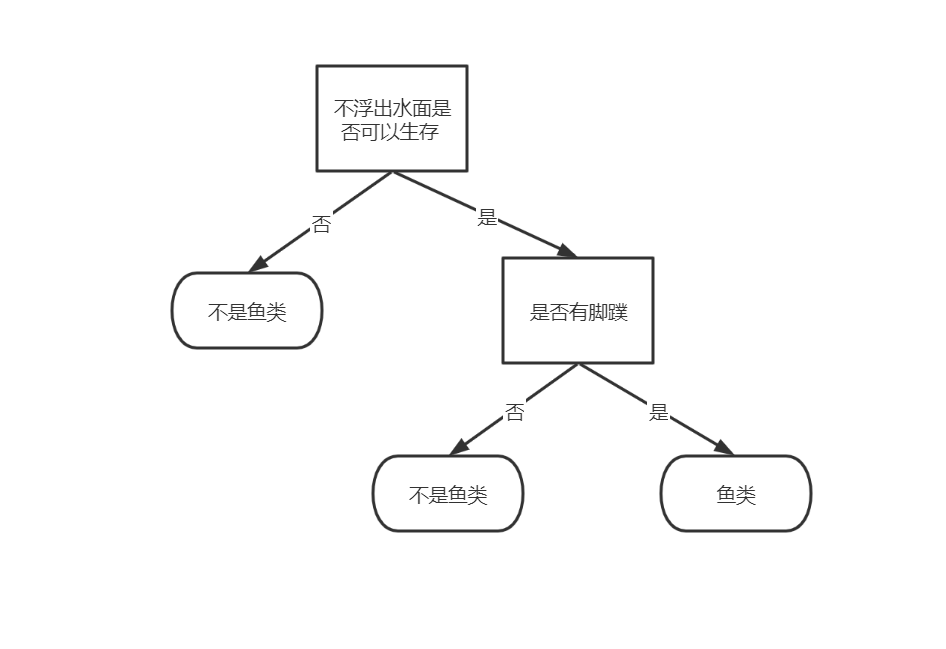
2.先按特征“ 是否有脚蹼 ”划分:
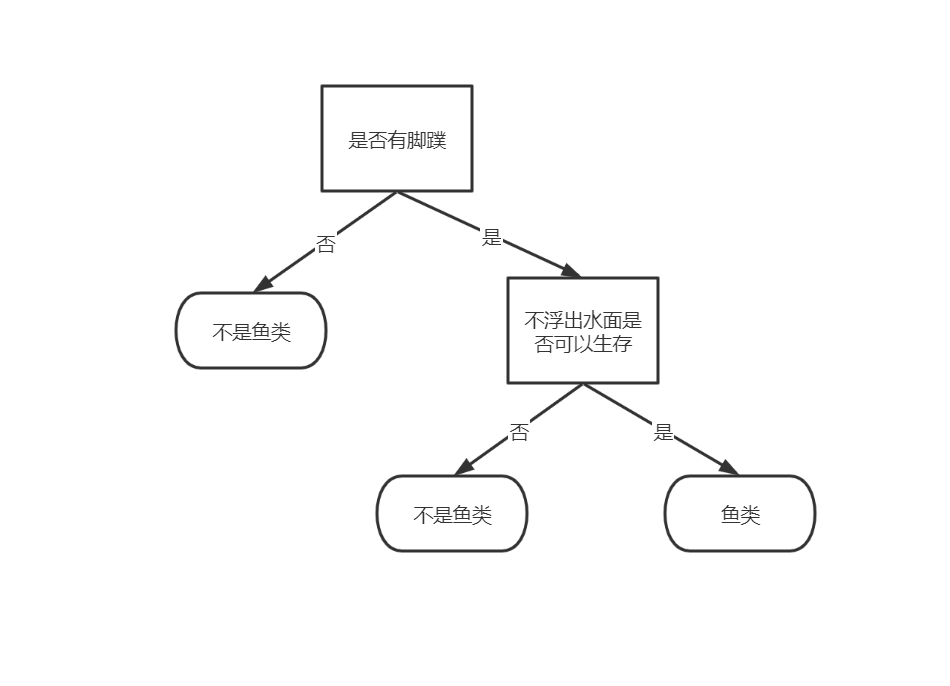
前几篇介绍的k-近邻算法可以完成很多分类任务,但是它最大的缺点就是无法给出数据的内在含义,决策树的主要优势就在于数据形式非常容易理解。
可以看到,按不同的顺序选取特征对数据集进行划分,构建出的决策树是不一样的。本篇就是介绍如何选取最佳的特征优先对数据集进行划分。
在上一节中我们已经知道了如何计算信息量和信息熵。而划分数据集的大原则是:将无序的数据变得更加有序。
在划分数据集之前之后信息发生的变化称为信息增益,知道如何计算信息增益,我们就可以计算每个特征值划分数据集获得的信息增益,获得信息增益最高的特征就是最好的选择。
接下来看我们的程序是如何选择最好的数据集划分方式的:
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 # the last column is used for the labels
baseEntropy = calcShannonEnt(dataSet) # 计算整体信息熵
bestInfoGain = 0.0 # 最佳信息增益
bestFeature = -1 # 最佳划分feature值
for i in range(numFeatures): # iterate over all the features
# i=0,featList=[1,1,1,0,0];i=1,featList=[1,1,0,1,1]
featList = [example[i] for example in dataSet] # create a list of all the examples of this feature
uniqueVals = set(featList) # get a set of unique values
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet) / float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet) # 计算平均信息熵期望
infoGain = baseEntropy - newEntropy # calculate the info gain; ie reduction in entropy
if (infoGain > bestInfoGain): # compare this to the best gain so far
bestInfoGain = infoGain # if better than current best, set to best
bestFeature = i
return bestFeature # returns an integer这个程序只有一个地方要注意,就是计算平均信息期望记得乘以权重prob,因为我们算出来的只是该特征值某一种取值的信息熵,应该乘以权重并累加全部的取值情况,才可以得到最后的信息期望:
newEntropy += prob * calcShannonEnt(subDataSet) # 计算平均信息熵期望执行的步骤如下:
第一步,计算整体信息熵,计算方法和上一篇介绍的是一样的,对于我们这个数据集,也就是
$$baseEntropy=-(\frac{2}{5}log_2\frac{2}{5}+\frac{3}{5}log_2\frac{3}{5})=0.9709505944546686$$
第二步,计算按不同特征划分数据集得到的信息期望(信息熵):
1.按特征“no surfacing 不浮出水面是否可以生存 ”划分:
(1)当“no surfacing”=0时,划分之后的数据集为[[1,”no”],[1,”no”]] ,可以计算出信息期望为
$$ H(“no surfacing”=0)=-log_21=0 $$
(2)当“no surfacing”=1时,划分之后的数据集为[[1,”yes”],[1,”yes”],[0,”no”]],可以计算出信息期望为
$$H(“no surfacing”=1)=-(\frac{2}{3}log_2\frac{2}{3}+\frac{1}{3}log_2\frac{1}{3}))= 0.9182958340544896 $$
所以,按特征 “no surfacing 不浮出水面是否可以生存 ”划分数据集,其平均信息期望为(注意乘以权重):
$$E(“no surfacing”)= \frac{3}{5}H(“no surfacing”=0)+\frac{2}{5}H(“no surfacing”=1)\\=0.5509775004326937$$
其信息增益$$G(“no surfacing”)=baseEntropy-E(“no surfacing”)=0.4199730940219749$$
2.同理,按特征“flippers 是否有脚蹼 ” 划分,可计算出其平均信息期望和信息增益为:
$$ E(“flippers”)=0.8$$
$$G(“flippers”)=0.17095059445466854$$
为了将无序的数据变得更加有序,我们应该优先选取那些信息增益大的特征对数据集进行划分,因此在本数据集中,我们优先选择“no surfacing” 进行划分。









评论 (0)